清尘
深度学习 Deep Learning
https://zh.d2l.ai/chapter_introduction/index.html
神经网络
人工神经网络（Artificial Neural Network，ANN或者简称NN），模仿生物神经网络结构和功能的计算模型。
神经元
神经网络核心单元是神经元（Neuron）
神经元模拟生物神经元的 “接收 - 处理 - 输出” 逻辑，结构如下：
-
输入：接收来自上一层的信号（如前一层神经元的输出 $x_1,x_2,…,x_n$）；
-
权重与偏置：每个输入对应一个可学习的权重 w1,w2,…,wn（表示输入的重要性），另有一个偏置 b（调整输出基线）；
-
激活函数：对 “加权和$ z=w_1x_1+w_2x_2+…+w_nx_n+b$” 做非线性变换，输出 $a=f(z)$（引入非线性，让网络能拟合复杂函数）。
常见激活函数 公式 特点 适用场景 ReLU $f(z) = \max(0, z)$ 计算简单、缓解梯度消失，稀疏激活 隐藏层（如 CNN、MLP） Sigmoid $f(z) = \frac{1}{1 + e^{-t}}$ 输出映射到 (0,1)，表示概率 二分类输出层 Softmax $f(z_i) = \frac{e^{z_i}}{\sum_j e^{z_j}}$ 输出映射到 (0,1) 且和为 1，表示多类别概率 多分类输出层 Tanh $f(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}$ 输出映射到 (-1,1)，中心对称 RNN 隐藏层（早期）
网络结构
- 输入层（Input Layer）：接收原始数据，不做计算（如图像任务输入 “像素矩阵”，文本任务输入 “词向量”）
- 隐藏层（Hidden Layer）：核心特征抽象层，层数≥1（“深度” 即指隐藏层数量），层数越多，能学习的特征越复杂（如 10 层网络可学习 “物体语义”，100 层网络可学习 “场景逻辑”）
- 输出层（Output Layer）：输出任务结果，维度由任务决定（如二分类输出 1 个值，10 分类输出 10 个值）
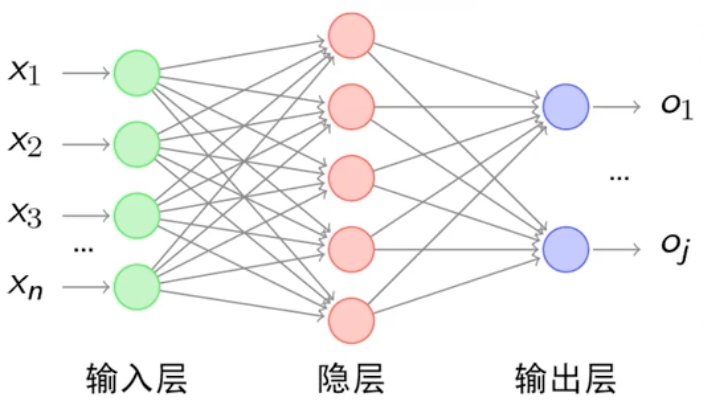
每个小圆圈代表一个神经元，隐藏层和输出层由输入的数据计算后输出，输出层神经元只是输入
特点
- 每个连接🔗之间都有个权值
- 同一层的神经元之间没有连接
- 最后输出结果对应的层也叫全连接层
线性神经网络
线性回归/单层神经网络
将线性回归模型描述为一个神经网络，如图（隐去了权重和偏置的值，只显示连接）：
输入为$x_1, \ldots, x_d$， 因此输入层中的输入数（或称为特征维度，feature dimensionality）为$d$。 网络的输出为，因此输出层中的输出数是1。 需要注意的是，输入值都是已经给定的，并且只有一个计算神经元。 由于模型重点在发生计算的地方，所以通常我们在计算层数时不考虑输入层。 也就是说，上图神经网络的层数为1。 我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络，或称为单层神经网络。
对于线性回归，每个输入都与每个输出（在上图有两个，在下图中只有一个输出）相连， 上图、下图的输出层称为全连接层（fully-connected layer）或称为稠密层（dense layer）。
线性回归可以理解为：预测明天的精确温度是 25.3°C 还是 26.1°C。预报 25.3°C 但实际是 26.1°C 是有误差的，追求的是平均误差最小。
softmax回归
softmax回归也是一个单层神经网络（拥有多个线性回归）
$$
\hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o})\quad \text{其中}\quad \hat{y}_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)}
$$
尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。 因此，softmax回归是一个线性模型（linear model）。
感知机
PLA：Perceptron Learning Algorithm
$$
u = \sum_{i=1}^{n} w_{i}x_{i} + b\\y = sign(u) = \begin{cases} +1, & u > 0 \\-1, & u \leq 0 \end{cases}
$$
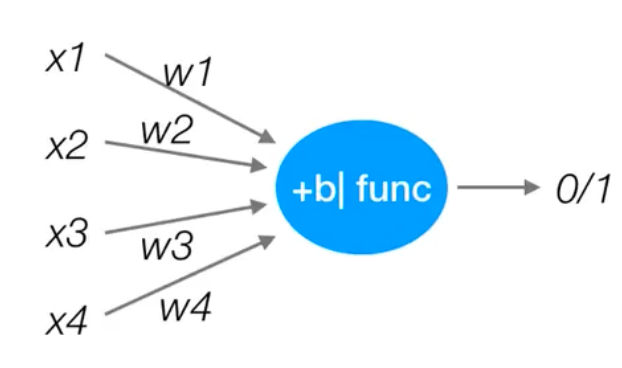
感知机是一种最基础的分类模型，类似于逻辑回归，不同的是，感知机的激活函数是
sign，逻辑回归用的是sigmoid。对比
- 线性回归模型：$f(x) = w \cdot x + b$
- 感知机模型：$f(x) = \text{sign}(w \cdot x + b)$，sign 是符号函数（当输入大于 0 时输出 1，小于等于 0 时输出 - 1）
- 逻辑回归模型：$f(x) = \text{sigmoid}(w \cdot x + b)$，sigmoid函数是$\sigma(z) = \frac{1}{1 + e^{-z}}$，把线性模型输出的任意实数$(-\infty, +\infty)$（压缩到 (0, 1) 区间，结果可直接解释为 “样本属于正类的概率”（如输出 0.8 表示有 80% 的概率是正类）。
单个感知机可以解决或、与问题
多层感知机
multilayer perceptron，通常缩写为MLP
隐藏层
激活函数
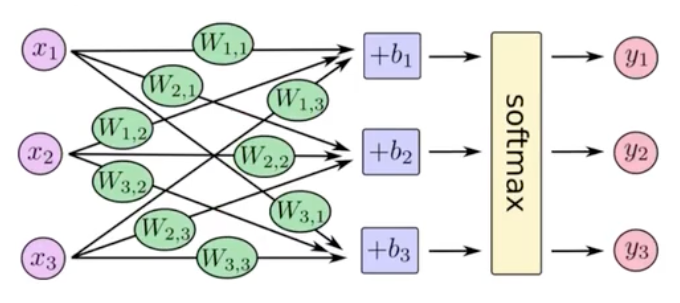
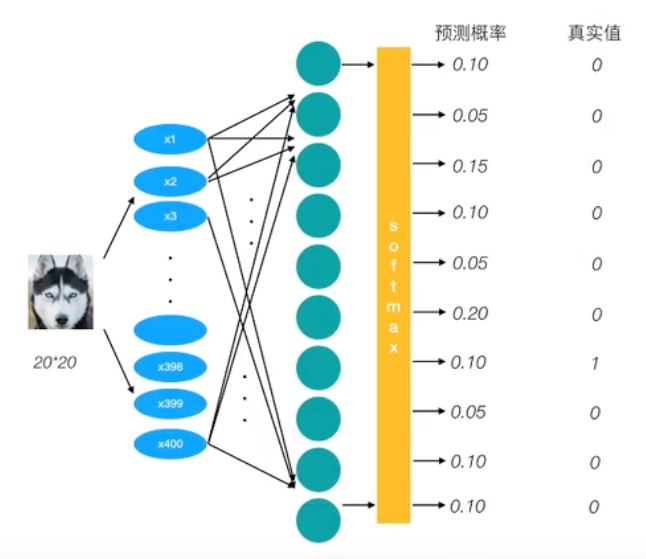
通过softmax函数，让神经网络输出变成了概率输出
损失函数
交叉熵损失
$$ H_{y’}(y) = -\sum_{i} y’_i \log(y_i) $$
优化函数
SGD
对比
| 特性 | 线性回归 | 逻辑回归 | Softmax回归 | 感知机 | 多层感知机 |
|---|---|---|---|---|---|
| 任务类型 | 回归 |
二分类 |
多分类 |
二分类 |
分类、回归（万能近似） |
| 输出 |
连续的数值（任意实数） |
一个概率值（0到1之间） |
一个概率分布（所有类别概率之和为1） |
离散的类别标签（+1/-1 或 1/0） |
由输出层决定： - 一个值（回归） - 一个概率（二分类） - 一个概率分布（多分类） |
| 目标 | 最小化预测值与真实值的差距（拟合数据）。 |
最大化观测样本的似然函数，即让预测概率尽可能接近真实标签。 |
同逻辑回归，但扩展到多个类别。 | 找到一个能完全分开两类数据的超平面（只要分类正确即可）。 |
通过多层非线性变换，学习数据中复杂的非线性映射关系。 |
| 激活函数 |
无（线性函数） |
Sigmoid函数（将输出压缩到(0,1)） |
Softmax函数（将多个输出归一化为概率分布） |
阶跃函数（如Sign函数） |
隐藏层：使用非线性函数（如ReLU, Tanh）。 输出层：根据任务选择（无/Sigmoid/Softmax）。 |
| 几何解释 | 寻找最佳拟合线（或超平面）。 | 寻找最佳决策边界，输出的是到边界距离的概率化结果。 | 寻找多个线性决策边界。 | 寻找一个决策边界，只关心数据点在边界的哪一侧。 | 通过组合多个简单边界，来学习复杂的曲线或曲面决策边界。 |
| 损失函数 |
均方误差 - 衡量预测值的错误程度。 |
对数损失/二元交叉熵 - 衡量预测概率分布与真实分布的差异。 |
交叉熵损失 - 对数损失的多分类推广。 |
感知机损失 - 只对分错的样本进行惩罚，且惩罚度固定。 |
由输出层决定，通常是对应任务的损失函数（如MSE、交叉熵）。 |
| 核心关系 | 基础模型 | = 线性回归 + Sigmoid | = 多输出线性回归 + Softmax（可看作逻辑回归的多分类版） | = 线性回归 + 阶跃函数（硬分类，而非概率输出） | = 上述任一模型 + 隐藏层 + 非线性激活函数 |
案例
//TODO：mnist手写体识别 （1.softmax回归，2.mlp）
体验
https://playground.tensorflow.org
卷积神经网络
加入了更有效的特征学习
应用场景
| 数据形态 | 视为“图像” | 典型应用 |
|---|---|---|
| 图像 | 天然的2D网格（像素） | 图像分类、目标检测 |
| 文本 | 1D网格（词序列）或2D网格（字符图） | 情感分析、垃圾邮件过滤 |
| 时间序列 | 1D网格（时间步） | 股价预测、心电图分析 |
| 图数据 | 非规则网格（需要特殊处理） | 社交网络分析、药物发现 |
| 棋盘游戏 | 2D网格（棋盘格子） | 围棋、国际象棋AI |
网络结构
- 卷积层：在原始图像上平移提取特征
- 激活层：增加非线性分割能力（激活函数）
- 池化层：减少学习参数，降低网络复杂度
- 全连接层
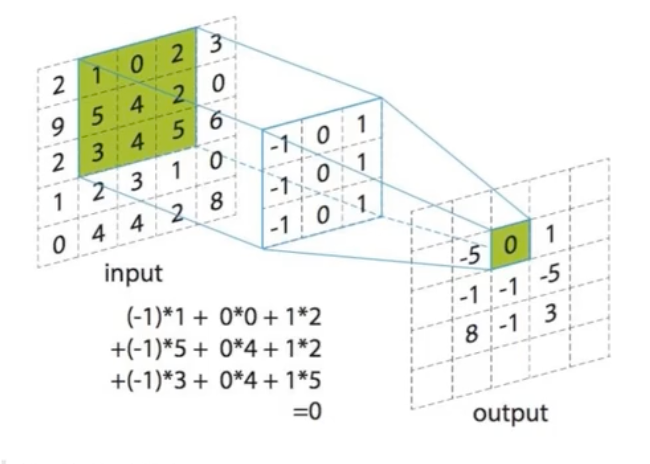
卷积层
卷积核
- 数量
- 大小
- 步长
- 0填充大小
池化层
pooling主要是特征提取
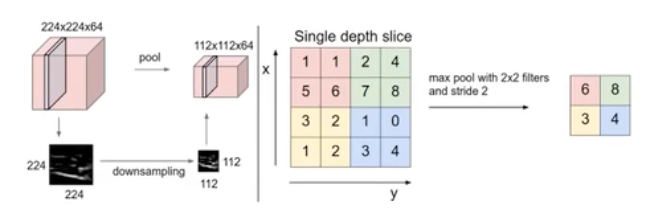
- 最大池化
- 平均池化
案例
//todo mnist手写体识别、验证码识别
TODO
Dropout
前向传播
反向传播
反向传播是 “计算梯度、更新参数” 的核心算法，遵循 “链式法则”—— 从输出层到输入层，逐层计算损失函数对每个参数的梯度，再通过优化器更新参数。
流程：
- 前向传播（Forward Pass）：输入数据通过网络，计算各层输出和最终损失 L；
- 反向传播（Backward Pass）：从输出层开始，计算 L 对输出层参数的梯度 → 隐藏层参数的梯度 → 输入层参数的梯度（链式法则）；
- 参数更新（Parameter Update）：用优化器根据梯度调整参数（如 w=w−η⋅∂w∂L，η 为学习率）。
梯度：损失函数对各个参数的偏导数集合