前言

课程链接：Language Modeling from Scratch

recap：扼要重述；概括；简要回顾；重述要点；<新闻>简明新闻；胎面翻新的轮胎新闻>

variations：变化，变更，变异；变体；变种；变奏曲；变奏；变异的东西

empirically：凭经验

evidence：证据

monolingual：单语的

multilingual：多语言的

rule of thumb：经验法则，粗略估算;经验之谈

theme：

  • the best way to learn is hands-on experience
  • the second best way is to try to learn from others’ experience

Start

标准的transformer的选择：

  • 位置编码
  • 激活函数：ReLU
  • 归一化方式：post-norm（后归一化），LayerNorm（层归一化）

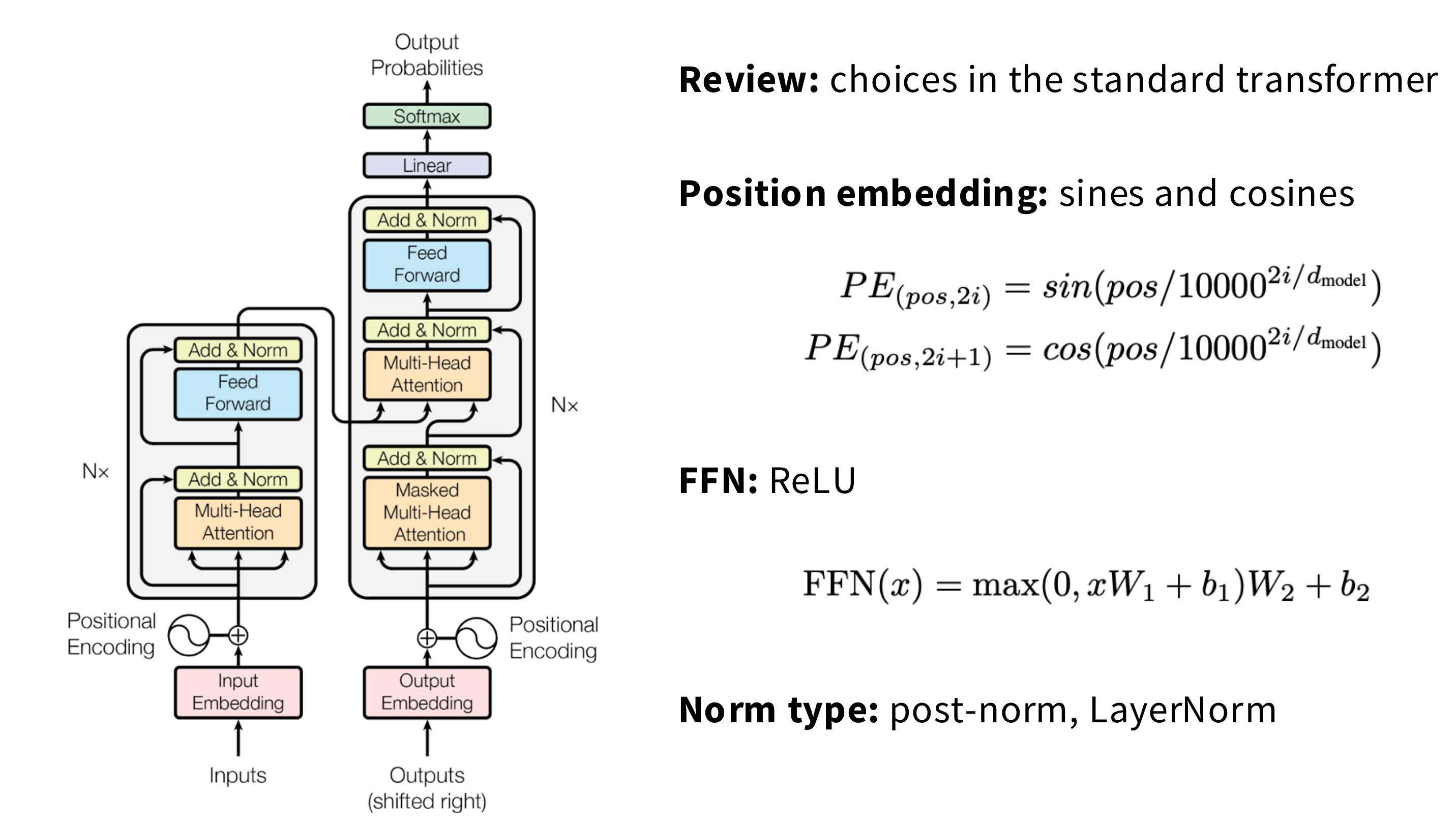
image-20250725140017941

我们要实现的是：简单、现代变体

  • 归一化方式：pre-norm（前归一化）
  • 旋转位置编码：RoPE（Rotary position embeddings）
  • 激活函数：SwiGLU
  • 线性层和层归一化没有偏移项

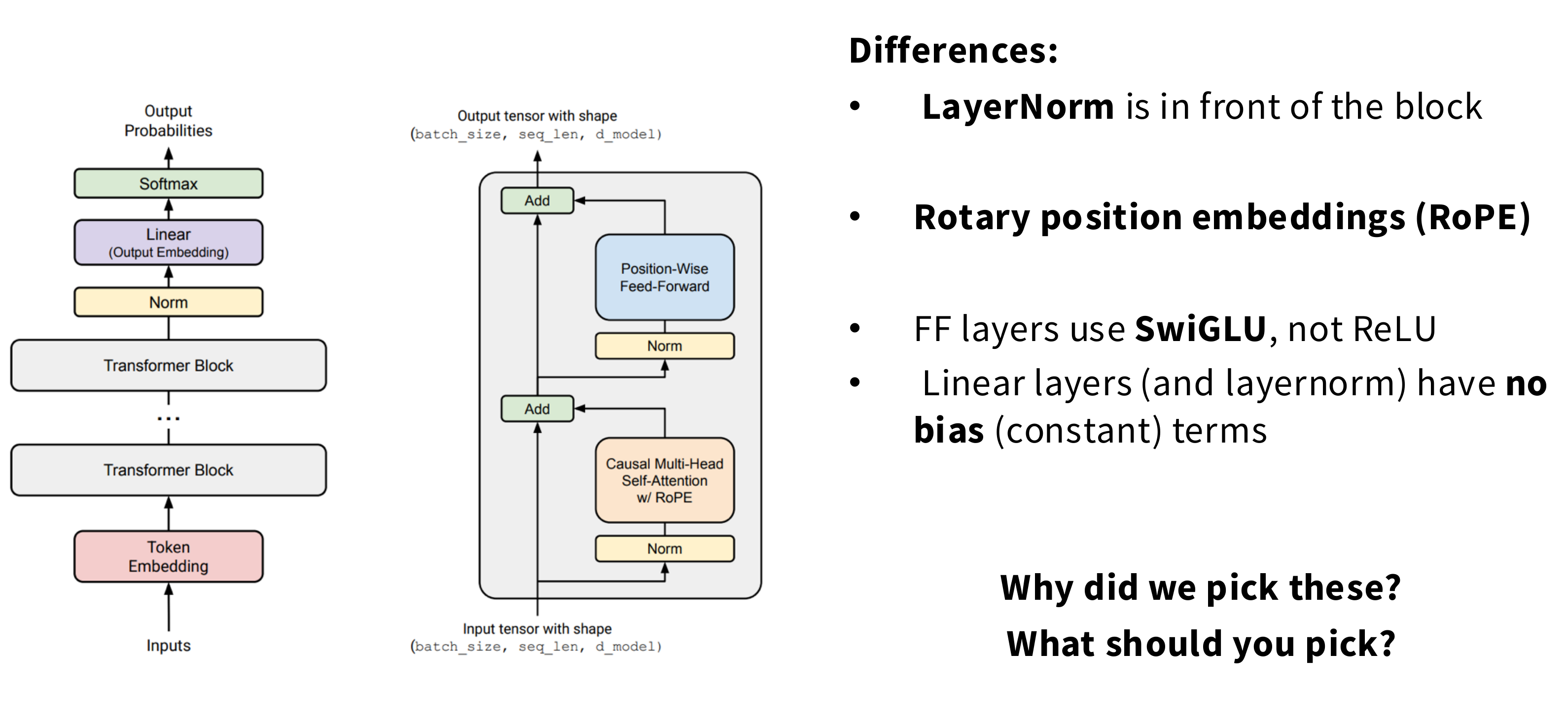
image-20250725140550503

现在的模型架构：

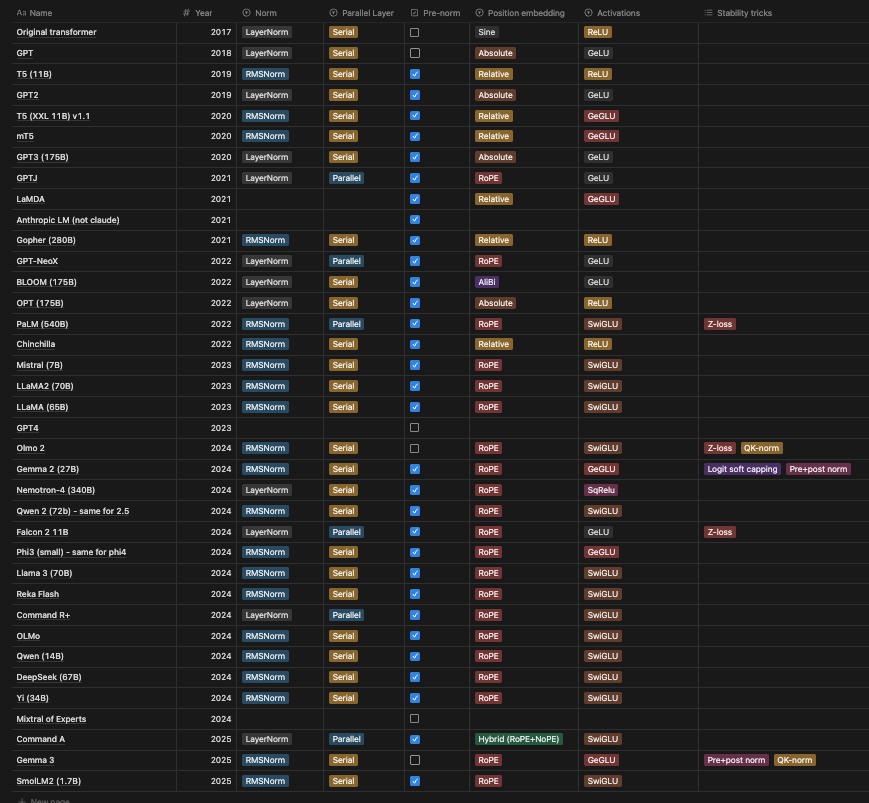
image-20250725141138541

上面这张PDF里面本身就好模糊

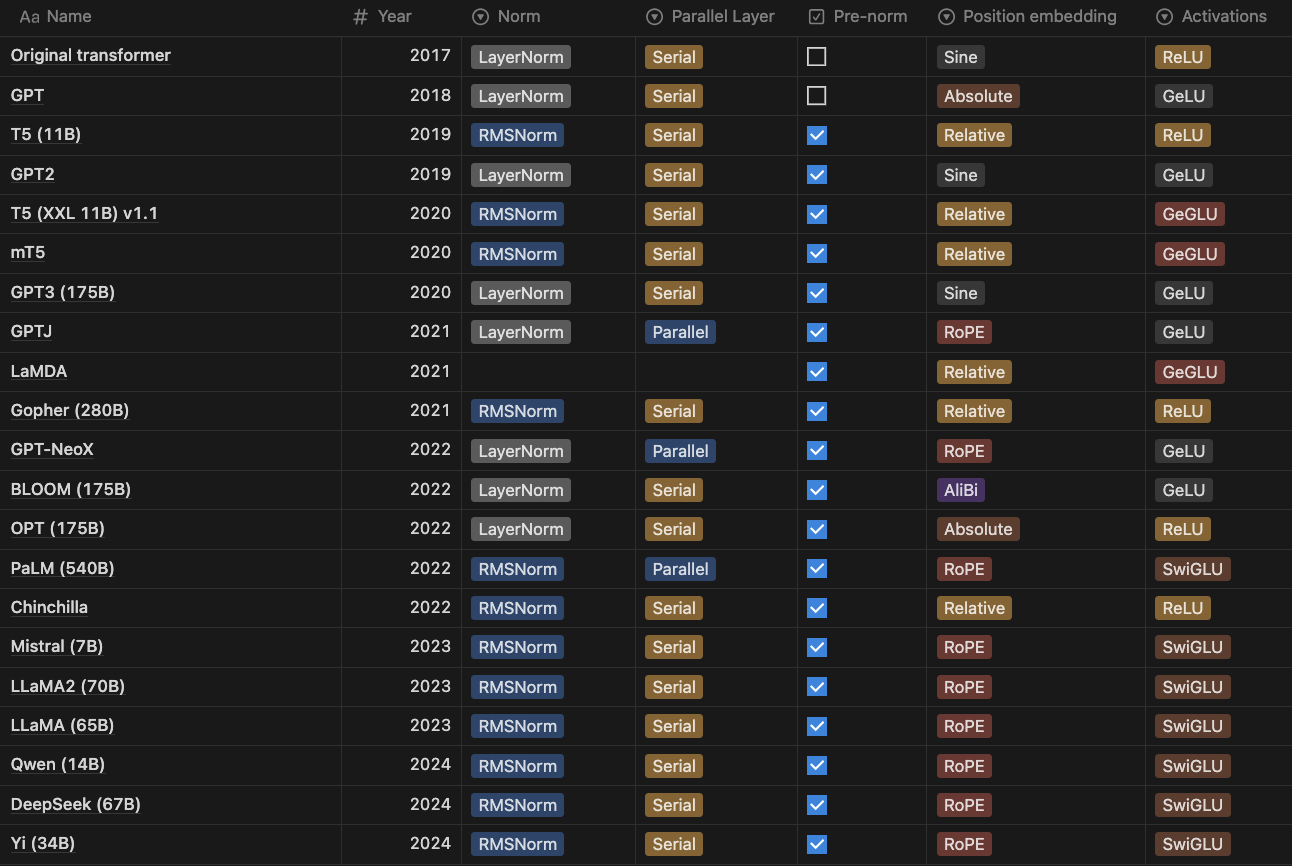
image-20250725141540425

High level view:

  • Low consensus(except pre-norm)低共识，除了前归一化
  • Trends toward ‘LLaMA-like’ architectures 都是LLaMA的架构趋势

归一化

前VS后

  • 后：x → sublayer → +x → LayerNorm → next sublayer
  • 前：x → LayerNorm → sublayer → +x → next sublayer

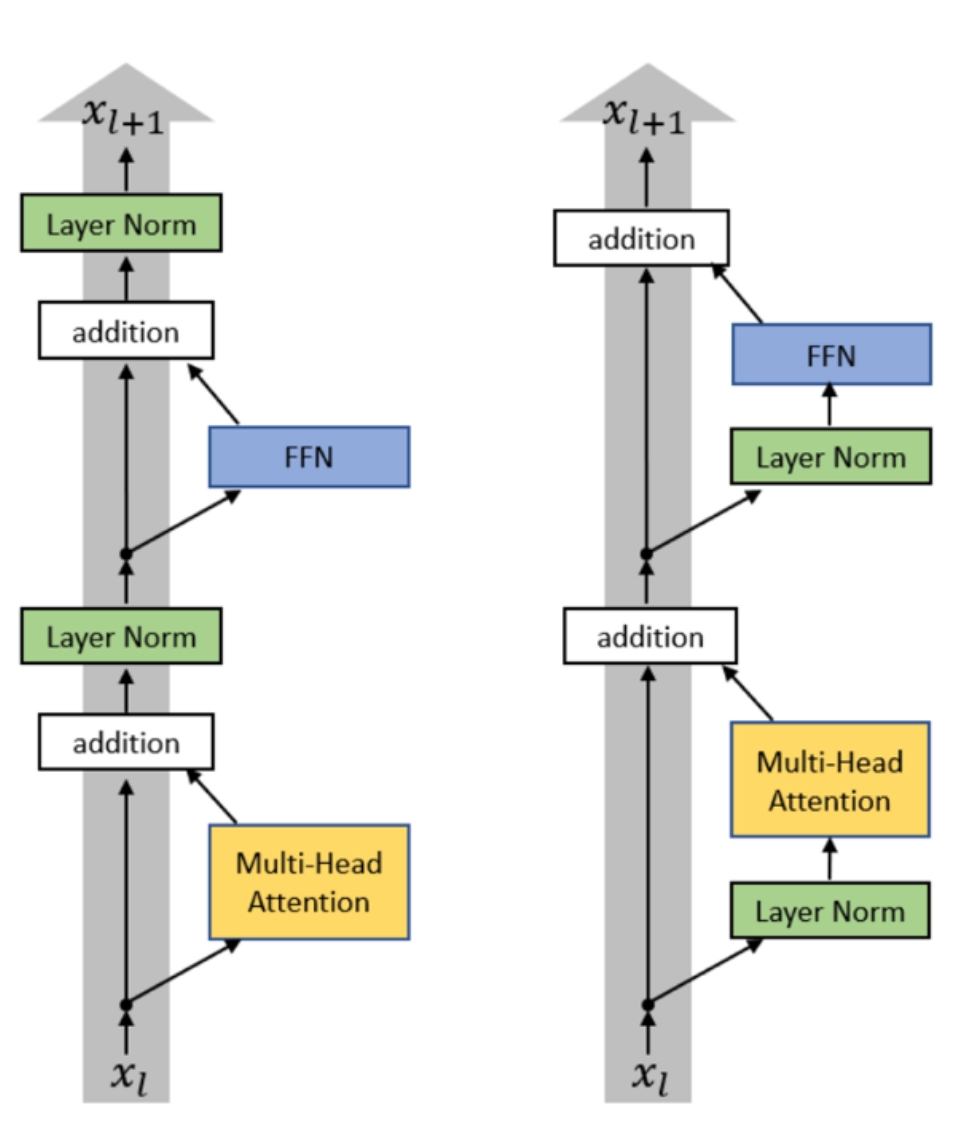
image-20250725141949541

Set up LayerNorm so that it doesn’t affect the main residual signal path (on the left)

设置LayerNorm，使其不影响主剩余信号路径（在左侧）

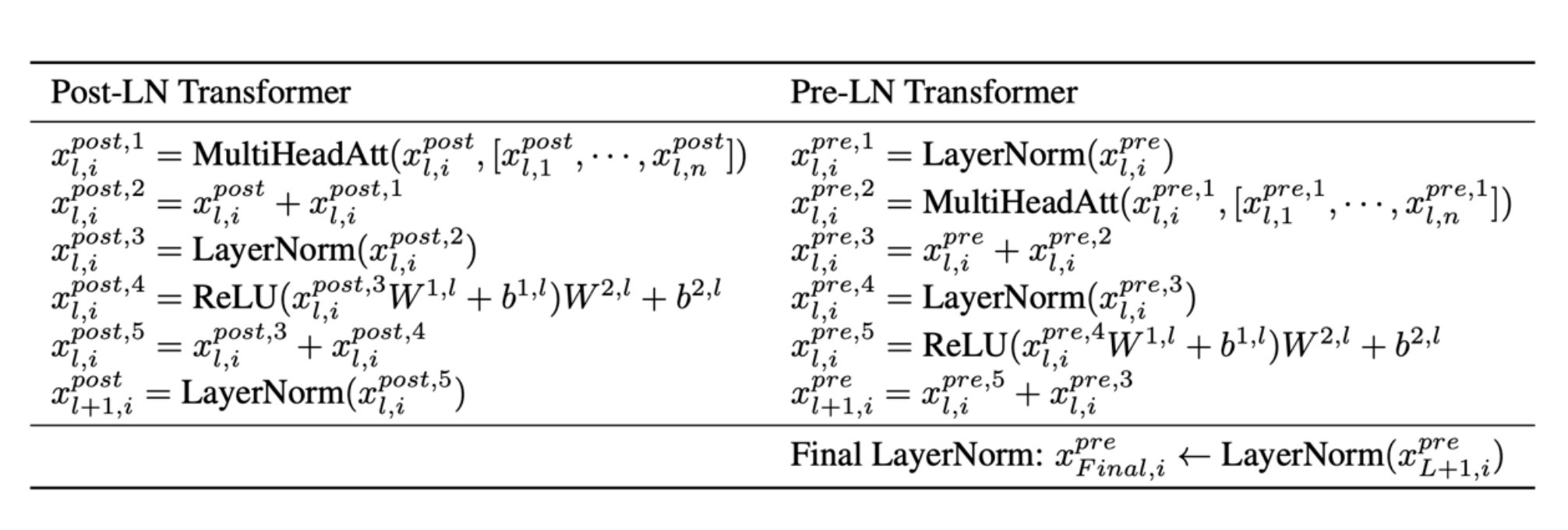
image-20250725142104028

  • Original stated advantage – removing warmup 早期大家把 LayerNorm 放在残差支路的“后面”（Post-LN，后归一化），理由是：只要把输出直接归一化，就能把方差压到 1，理论上就不再需要“学习率 warmup”。
  • Today – stability and larger LRs for large networks 可到了今天，人们更喜欢把 LayerNorm 放在残差支路的“前面”（Pre-LN，前归一化）。因为真正训超大模型时，Post-LN 依然容易梯度爆炸/消失，Pre-LN 反而更稳，还能用更大的学习率。
维度 Post-LN Pre-LN
深层梯度 容易vanishing消失 近似恒等映射，梯度更稳
学习率 需要小 LR + warmup 可以直接上较大 LR
大模型训练 需要大量调参防崩 几乎“开箱即用”
最终性能 稍好（早期小模型） 差异极小，训练效率远高于性能差异

双层归一化

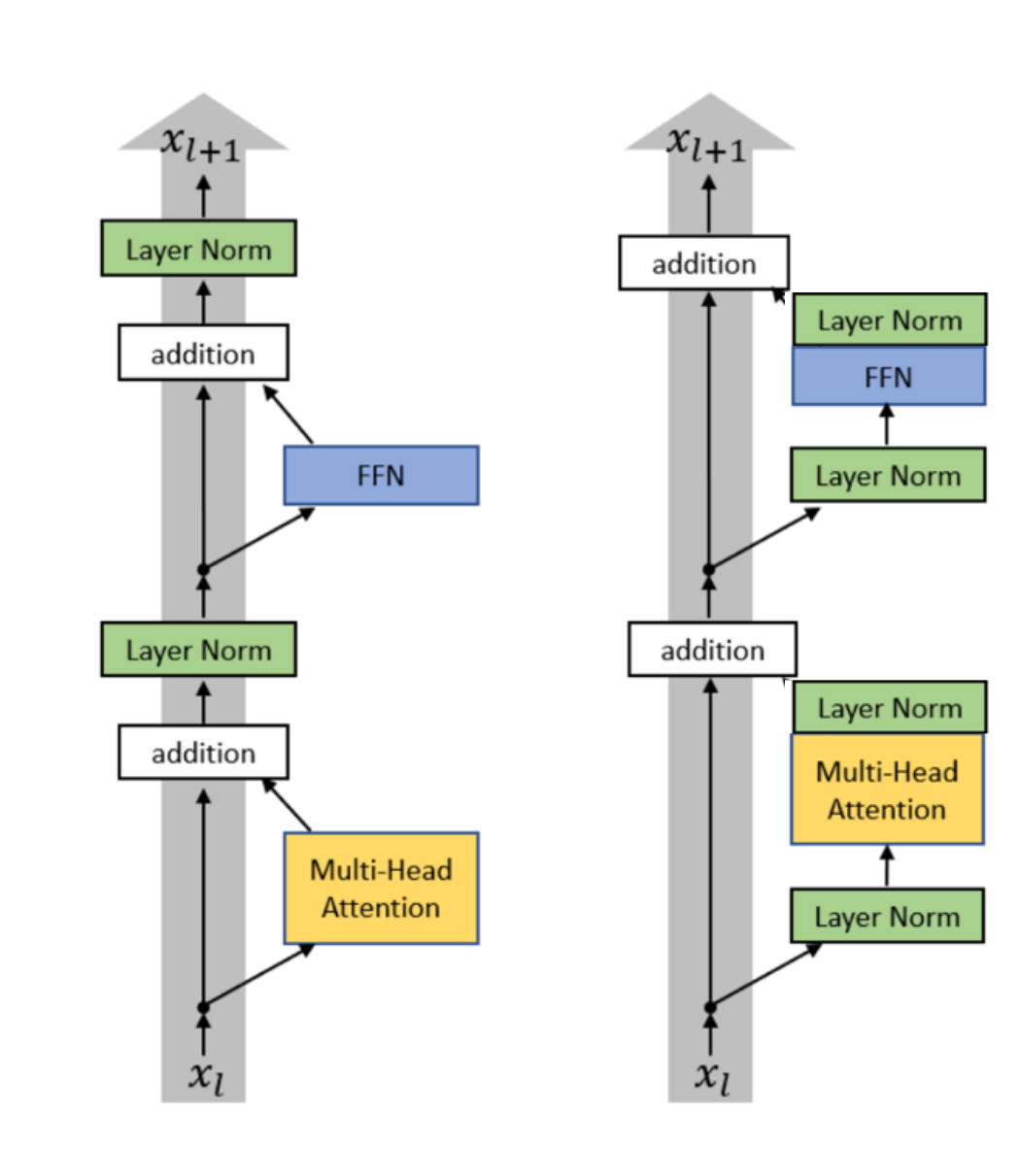
image-20250725142723389

Recent models: Grok, Gemma 2. Olmo 2 only does non-residual post norm

LayerNorm vs RMSNorm

层归一化

平均值和方差 $$ y=\frac{x-E[x]}{\sqrt{Var[x]+\epsilon}}*\gamma+\beta $$ $\epsilon$：诶噗色隆是小常数（防止除0）

$\gamma$：伽马是可学习参数

$\beta$：贝塔也是可学习参数

RMSNorm

LN的均值 μ 为0时便是RMSNorm

（Root Mean Square Normalization） $$ RMSNorm(x)=\frac{x}{RMS(x)}·\gamma，其中RMS(x)=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{x_i^2} } $$ RMSNorm计算更少，存的参数也更少，因为没有bias $$ y= \frac{x}{\sqrt{\left | \left | x \right | \right |_2^2+\epsilon }}*\gamma $$ 代码示例：

import numpy as np

x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=float)

# 1. LayerNorm (无学习参数 γ, β 时)
mu = x.mean()
var = x.var(ddof=0)
layer_norm = (x - mu) / np.sqrt(var + 1e-8)   # 1e-8 防止除零

# 2. RMSNorm (无学习参数 γ 时)
rms = np.sqrt(np.mean(x ** 2))
rms_norm = x / (rms + 1e-8)

print("原始数据:   ", x)
print("LayerNorm: ", layer_norm)
print("RMSNorm:   ", rms_norm)

# 原始数据:    [1. 2. 3. 4. 5. 6. 7. 8. 9.]
# LayerNorm:  [-1.54919334 -1.161895   -0.77459667 -0.38729833 0.23434234  0.38729833 0.77459667  1.161895    1.54919334]
# RMSNorm:    [0.17770466 0.35540933 0.53311399 0.71081865 0.88852332 1.06622798 1.24393264 1.4216373  1.59934197]
特性 LayerNorm RMSNorm
均值中心化 减去均值 $\mu = \frac{1}{n}\sum x_i$ 省略（假设均值为0）
方差计算 基于中心化后的值 $\sum (x_i - \mu)^2$ 直接基于原始值 $\sum x_i^2$
参数 增益 $\gamma$ 和偏置 $\beta$ 仅增益 $\gamma$（通常无偏置）
计算效率 较低（需计算均值和方差） 较高（减少约7%训练时间）
性能 基准 在多数任务中与LayerNorm相当或更优

丢弃偏置项

dropping bias terms $$ FFN(x)=\sigma(xW_1)W_2 $$

Reasons: memory (similar to RMSnorm) and optimization stability

减少内存和优化器稳定

激活函数

激活函数全家桶：

ReLU, GeLU, Swish, ELU, GLU, GeGLU, ReGLU, SeLU, SwiGLU, LiGLU

ReLU

$$ FF(x)=max(0,xW_1)W_2 $$

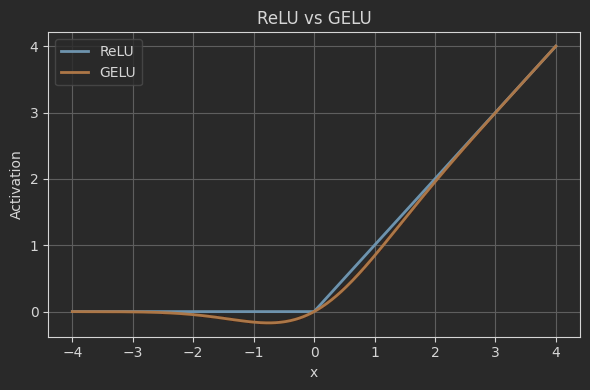
GeLU

$$ FF(x)=GELU(xW_1)W_2 $$

$$ GELU(x)=x·\Phi(x)=x·\frac{1}{2}[1+erf(\frac{x}{\sqrt{2}})] $$

  • Φ(x) 是高斯分布的累积分布函数（CDF）。
  • erf 是误差函数（error function）。

关键特性

  • 平滑性：处处可导，避免了ReLU的“硬截断”。
  • 非单调性：负半轴有微小输出（与ReLU不同）。
  • 概率解释：可视为对输入随机降权的期望（以概率Φ(x)保留x）。

image-20250725153321116

GLU

Gated Linear Unit的思想是：不是简单地用 ReLU 激活整个线性输出，而是引入一个“门控”机制，控制哪些信息可以通过。

原始 GLU 的形式一般是： $$ GLU(x)=(xW_1)⊗σ(xV)⋅W_2 $$

其中 ⊗ 是逐元素乘法（Hadamard 积），σ 是 sigmoid 函数，V 是另一个可学习的参数矩阵。门控信号由$σ(xV)$ 产生，用来调制$ xW_1 $​​的输出。

哈达玛积(Hadamard product)：若A=(aij)和B=(bij)是两个同阶矩阵，若cij=aij×bij,则称矩阵C=(cij)为A和B的哈达玛积，或称基本积

$$ \begin{bmatrix} a_{11}b_{11}& a_{12}b_{12}& …& a_{1n}b_{1n}& \\
a_{21}b_{21}& a_{22}b_{22}& …& a_{2n}b_{2n}& \\
\vdots& \vdots& \vdots& \vdots& \\
a_{m1}b_{m1}& a_{m2}b_{m2}& …& a_{mn}b_{mn}& \end{bmatrix} $$

ReGLU

使用 ReLU 而不是 sigmoid 来做门控 $$ FF_{ReGLU}(x)=(max(0,xW_1)⊗(xV))W_2 $$

GeGLU

$$ FFN_{GEGLU}(x,W,V,W_2)=(GELU(xW)\otimes xV)W_2 $$

SwiGLU

swish is x * sigmoid(x) $$ FFN_{SwiGLU}(x,W,V,W_2)=(Swish_1(xW)\otimes xV)W_2 $$

Note: Gated models use smaller dimensions for the 𝑑𝑓𝑓 by 2/3

在使用门控机制如 GLU、ReGLU、SwiGLU 等）的前馈网络（FFN）中，为了保持与标准 FFN 相当的参数量或计算量，通常会将中间层的维度$d_{ff}$​（即隐藏层宽度）设置为原来大小的约 2/3。

因为多了个$V$，假设 $d_{model}=1024$ ，标准 FFN 中 $d_{ff}=4096$：

  • 标准 FFN 参数（前两矩阵）：

    $1024×4096+4096×1024≈8.4M$

  • ReGLU 如果也用 $d_{ff}=4096$：

    • $W_1:1024×4096$
    • $V:1024×4096$
    • $W_2:4096×1024$
    • 总参数：3×(1024×4096)≈12.6M → 多了 50%！

  • 所以把$d_{ff} 改为 \frac{2}{3}×4096≈2730$

    • 参数变为：$2×(1024×2730)+2730×1024≈8.4M$

串行和并行层

image-20250729111836895

如果实现正确，LayerNorm可以共享，矩阵乘法可以融合

架构总结

image-20250729111758437

位置编码

RoPE

rotary position embeddings

看下苏神的文章：

  • https://kexue.fm/archives/8130
  • https://kexue.fm/archives/8231
  • https://kexue.fm/archives/8265
  • https://kexue.fm/archives/8397
  • https://papers.cool/arxiv/2104.09864

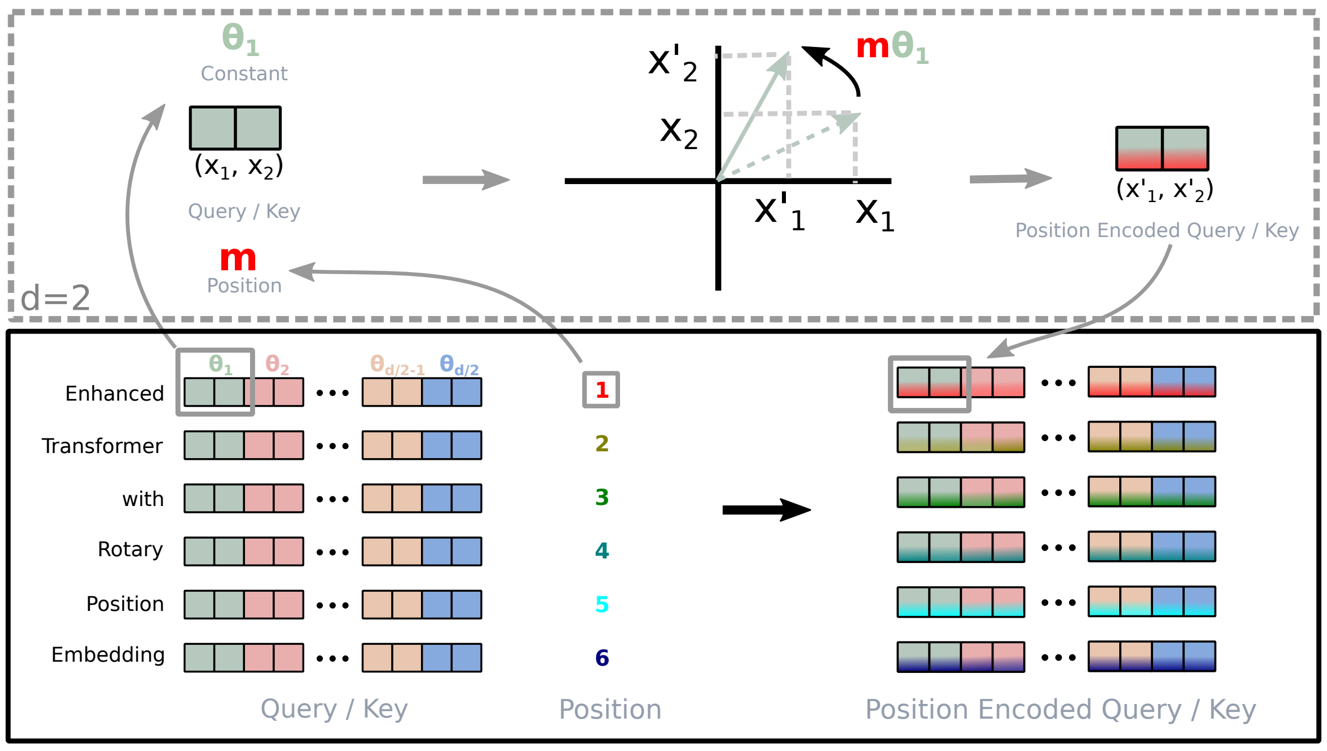
image-20250729134318233

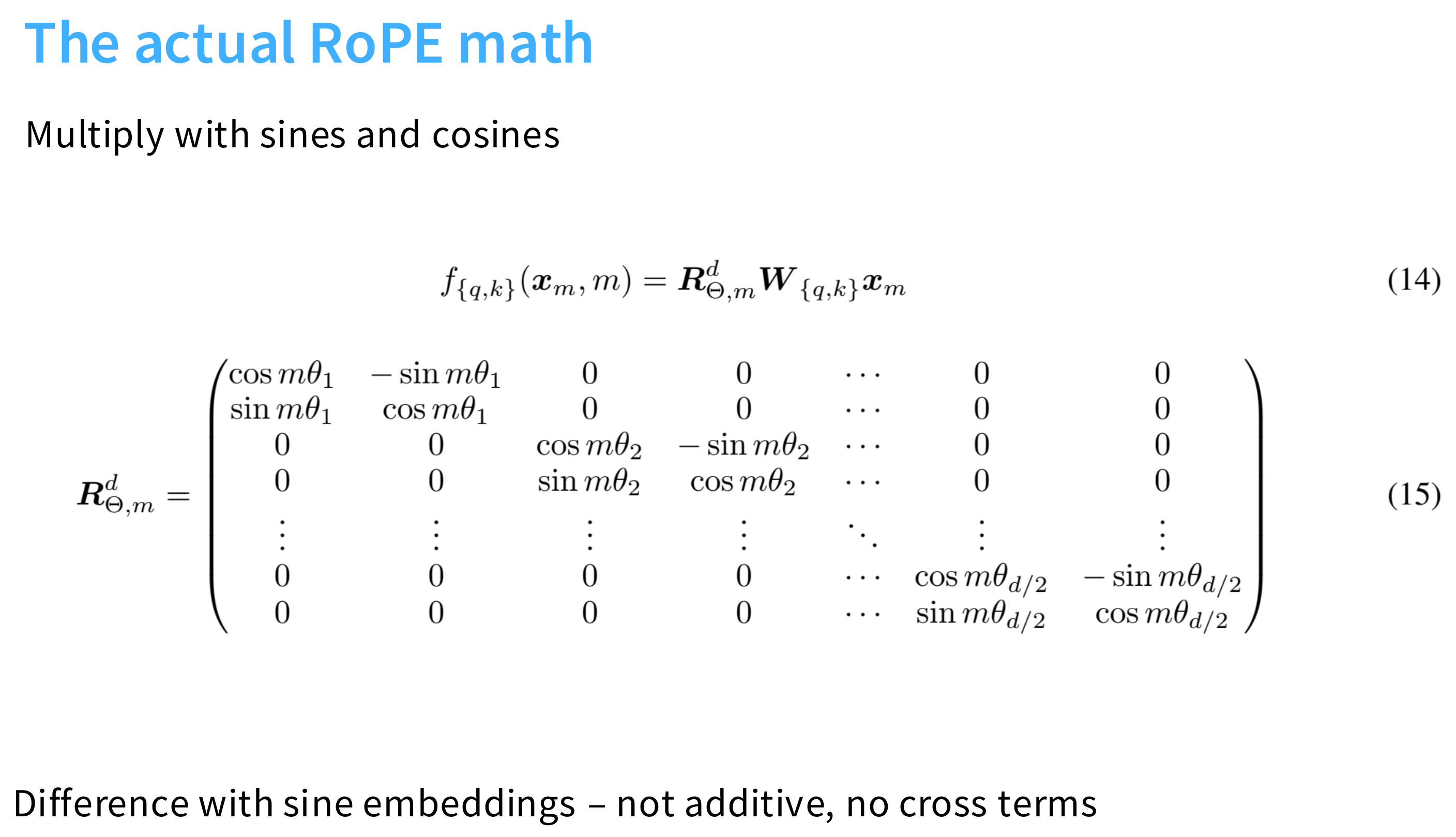
image-20250729134343092

image-20250729134353417

ok，短时间理解不了，后面再补！！！

超参数

讲了一些共识超参数consensus hyperparameters

前馈层-模型维度比例

Feedforward – model dimension ratio $$ d_{ff}=4d_{model} $$ 用了GLU的话，需要注意：

image-20250729135254020

还有一个大胆的T5用了64倍

image-20250729135444211

根据经验，这个超参数在1-10之间有一个盆地使loss最优

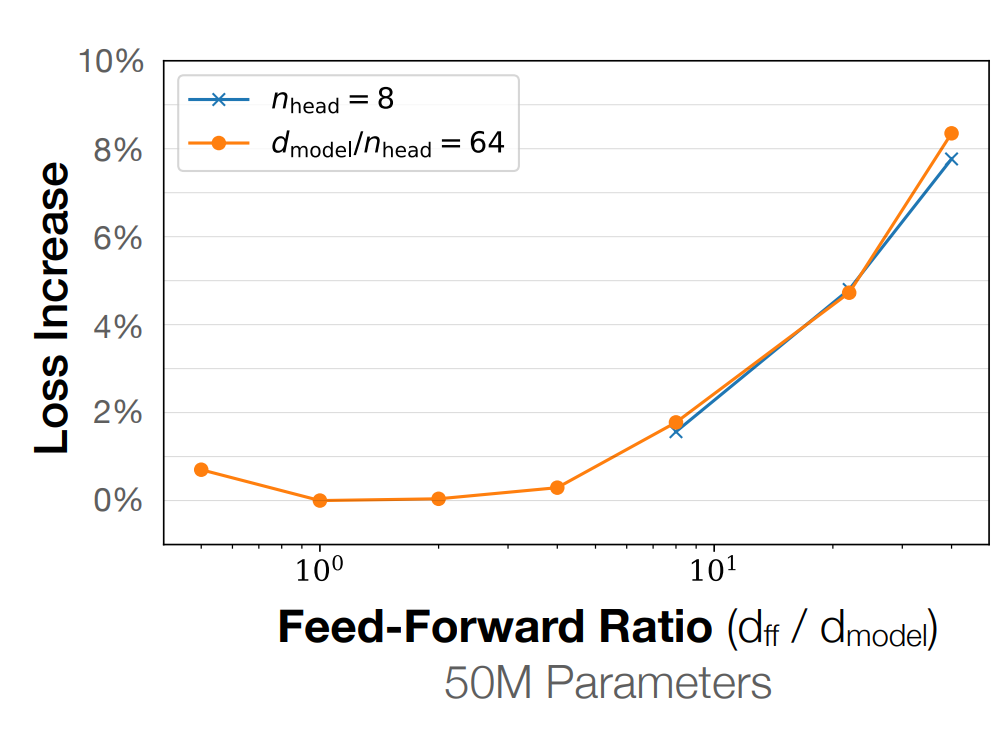
image-20250729135621779

多头注意力数量-模型维度比例

Head-dim * num-heads to model-dim ratio

我们可以有head-dimensions > model-dim / num-heads，但大多数模型确实遵循这一指导方针。

纵横比 - Aspect ratios

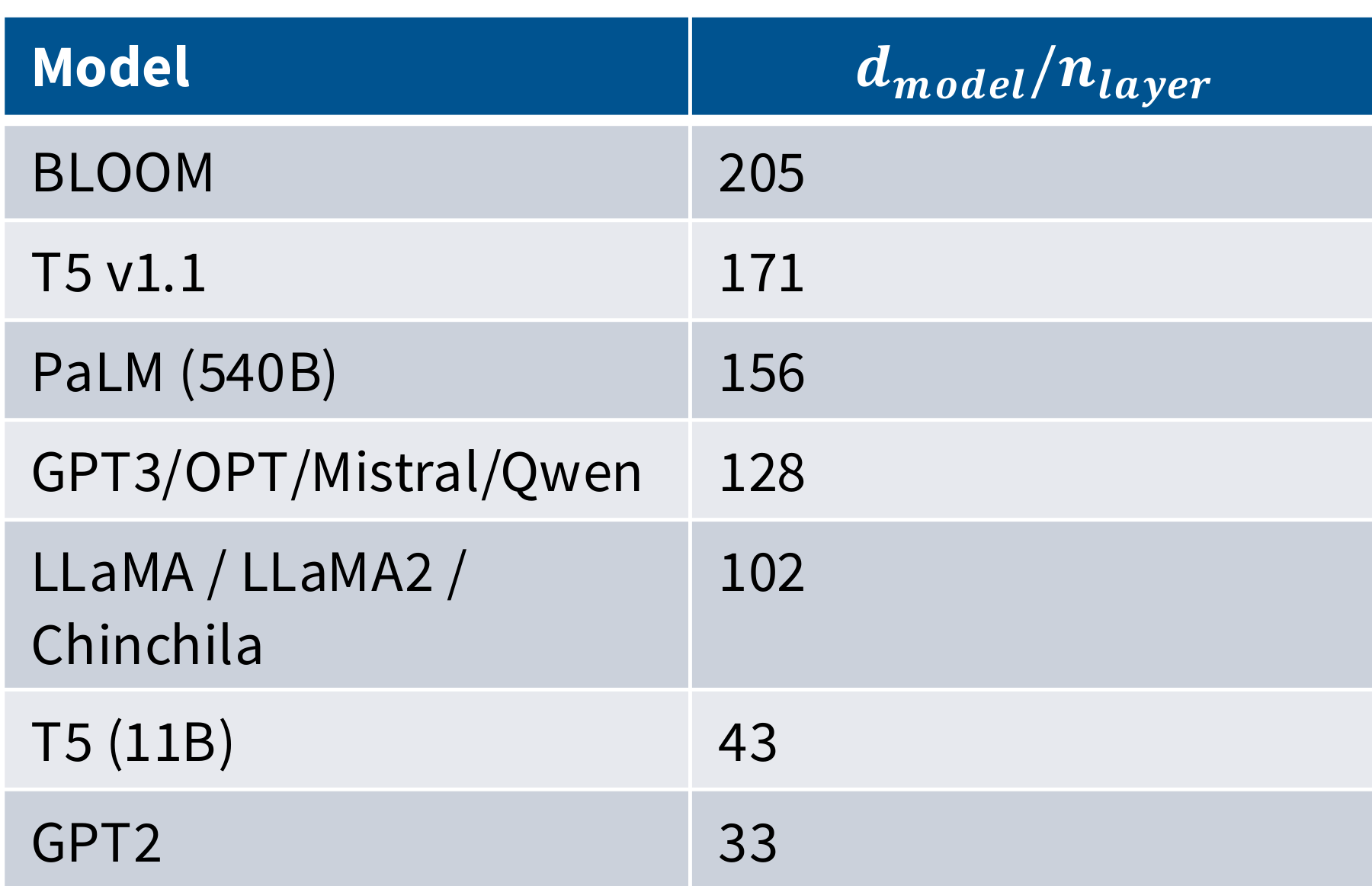
image-20250729140637771

极深的模型更难并行化，延迟也更高

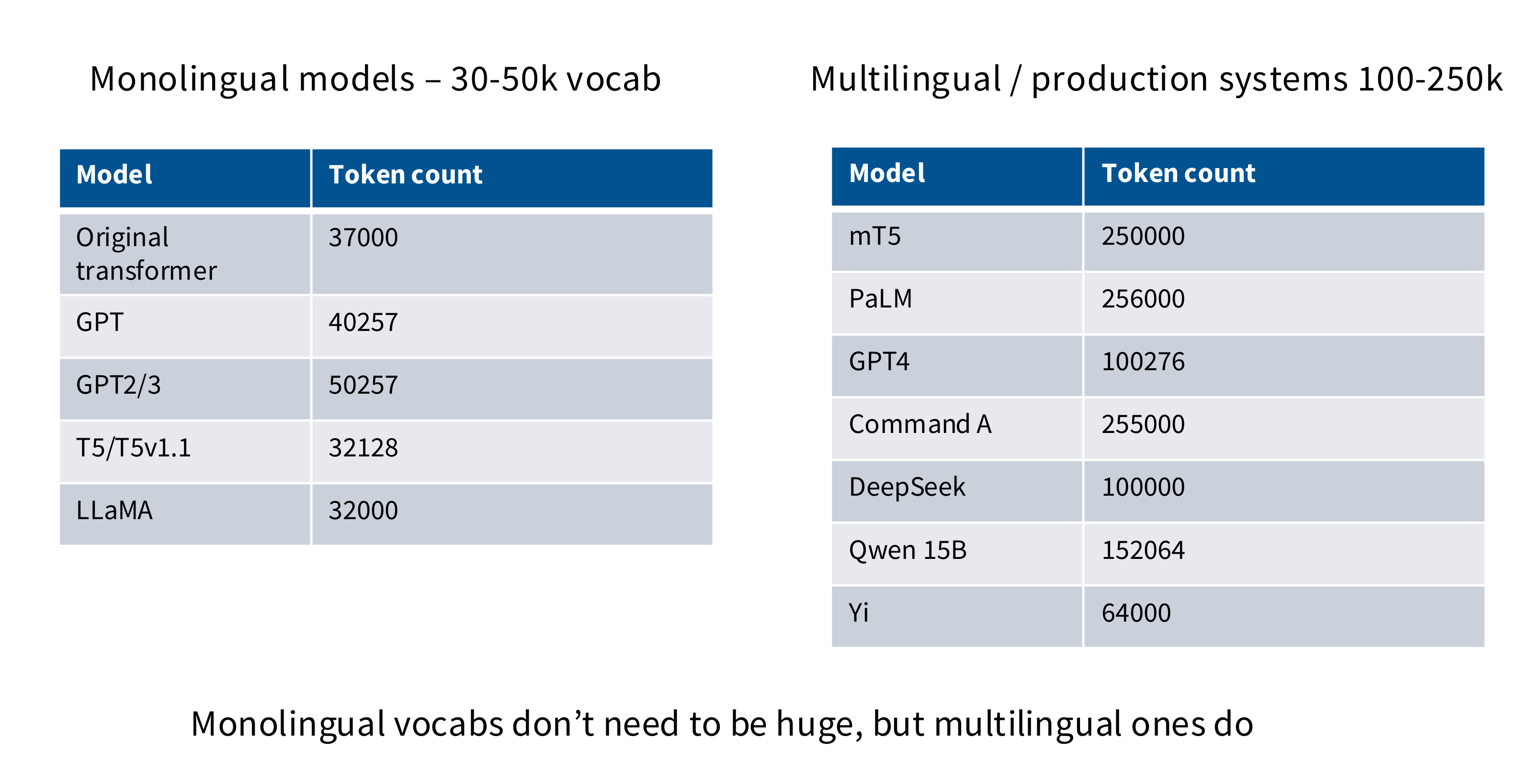
词表大小 - vocabulary sizes

image-20250729141140719

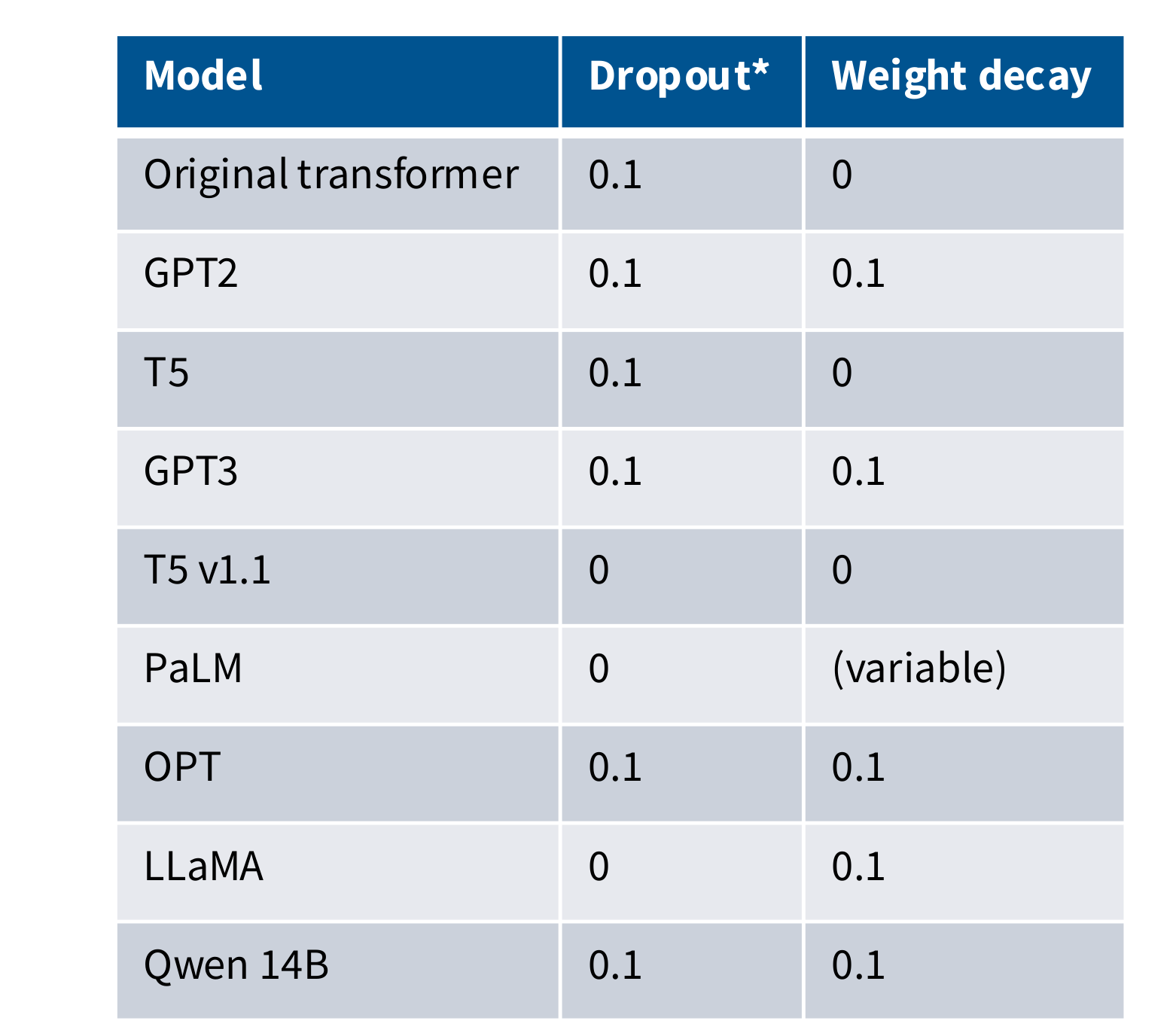
Dropout and other regularization

dropout和正则化

image-20250729141552104

总结

  • feedforward：经验都是4为标准
  • head dim：$d_{head} * N_{haed} = d_{model}$是标配，不过低一点也没验证行不行
  • aspect ratio：良好的值范围区间在100-200，太深硬件也跟不上
  • regularization：还是要正则化，but its effects are primarily on optimization dynamics

稳定性手段-Stability tricks

Softmaxes

Softmaxes – can be ill-behaved due to exponentials / divison by zero

Softmax可能由于指数/除以零而表现不佳

image-20250729142618960

Attention softmax stability – the ‘QK norm’

The query and keys are Layer (RMS) normed before going into the softmax operation.

在softmax之间对QK进行正则化。

Logit soft-capping

Logit Soft-Capping 是一种在大语言模型（LLM）推理阶段（或训练中）用于控制输出 logits 范围的技术，目的是抑制模型生成过于极端或重复的文本，提升生成质量。

它被用于一些先进模型中，比如 Google 的 Gemma、PaLM、LLaMA-3 的推理过程中，作为后处理 logits 的一种“软限制”手段。

image-20250729142927898

给定一个原始的 logit 值 z ，soft-capping 通过如下函数进行变换： $$ SoftCap(z)=c⋅tanh(\frac{z}{c}) $$ 其中：

  • z ：模型输出的原始 logit（某个词的得分）
  • c ：capping 值（例如 30 或 50），表示 logits 的“软上限”
  • tanh ：双曲正切函数，把输入压缩到 (−1,1) 区间，乘以 c 后压缩到 (−c,c)

所以最终输出的 logit 被“软性地”限制在 [−c,c] 范围内。

函数：$f(z)=c⋅tanh(z/c)$

输入z 输出f(z) 行为
很小（负很大） ≈ -c 趋近下界
0 0 不变
很大（正很大） ≈ c 趋近上界
中等大小 ≈ z 几乎无影响

特点：

  • 对中等大小的 logits 几乎不改变
  • 对极大或极小的 logits 进行“温和压制”，不让它们主导 softmax
  • 是平滑、可导的函数，不会破坏梯度（可用于训练）

在生成文本时，某些 token 的 logit 可能非常大（比如某个词被强烈偏好），导致：

  • softmax 后概率接近 1
  • 其他词几乎没机会被采样
  • 容易引发：
    • 重复生成（如“the the the”）
    • 多样性差
    • 幻觉增强（过度自信错误内容）

Soft-Capping

用 c=30 举例：

$SoftCap(100)=30⋅tanh(100/30)≈30⋅tanh(3.33)≈30⋅0.997≈29.9$

而原本是 100 → 现在被压到接近 30

这样在 softmax 中，它仍然很高，但不再压倒性地主导，其他合理词也有机会被采样。

Attention heads

标准的多头注意力中，每个头有独立的QKV

  1. 对于第i个头，计算： $$ Q_i=XW_i^Q,\ K_i=XW_i^K,\ V_i=XW_i^V $$

  2. 然后分别计算注意力： $$ Attention(Q_i,K_i,V_i) $$

  3. 最后将所有头的输出拼接并线性变换$W_O$​

现实为了减少实际的注意力消耗：

Reducing attention head cost GQA/MQA

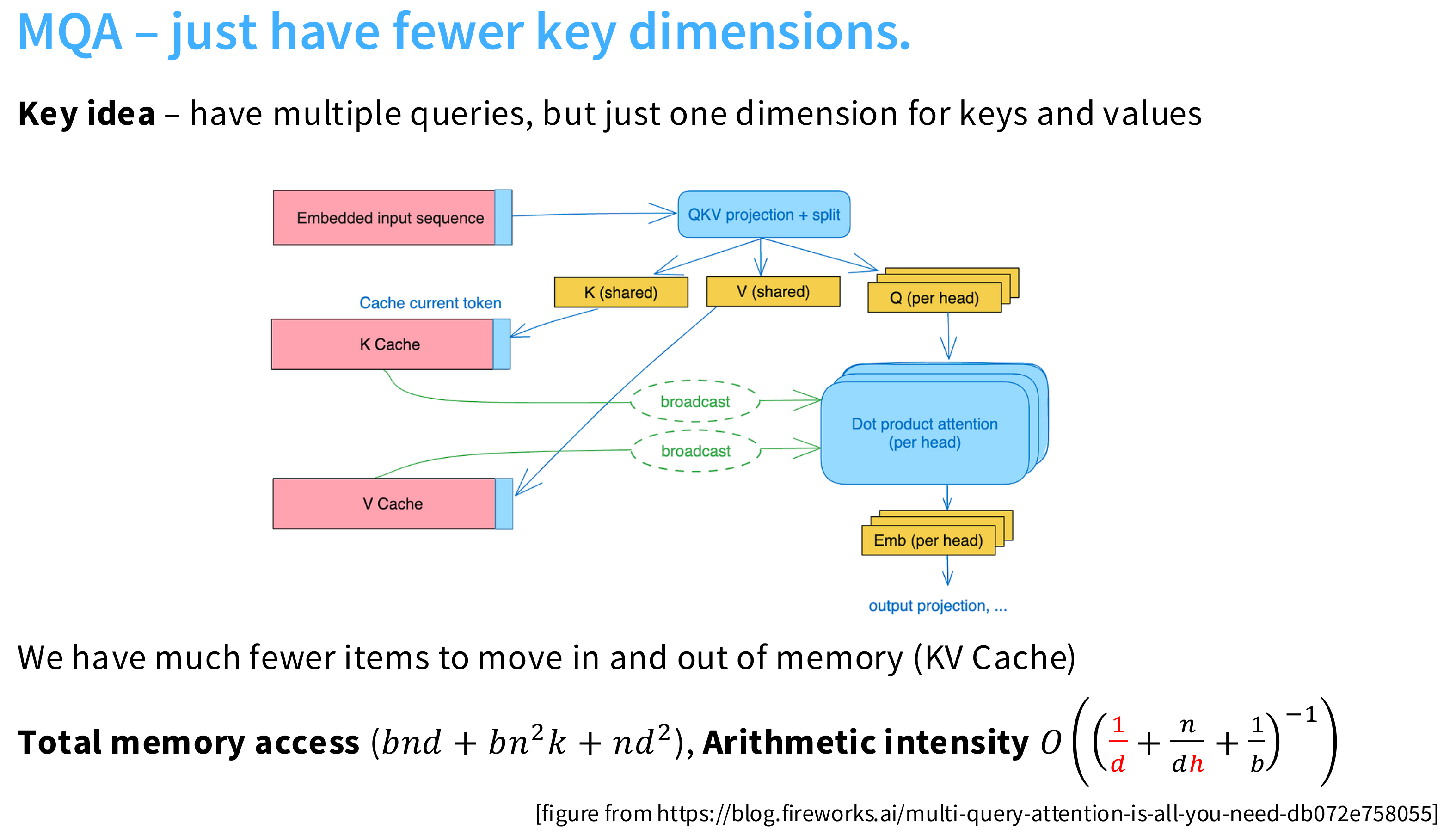
MQA（Multi-Query Attention）

所有注意力头共享同一个 K 和 V，但每个头仍然有自己的 Q。 $$ Q_i=XW_i^Q,\ K=XW^K,\ V=XW^V $$ K,V共用只有Q不一样。

缺点：

表达能力下降：因为所有头共享相同的 Key 和 Value，限制了模型的表达灵活性，可能影响模型质量（尤其在复杂任务上）。

image-20250729144712709

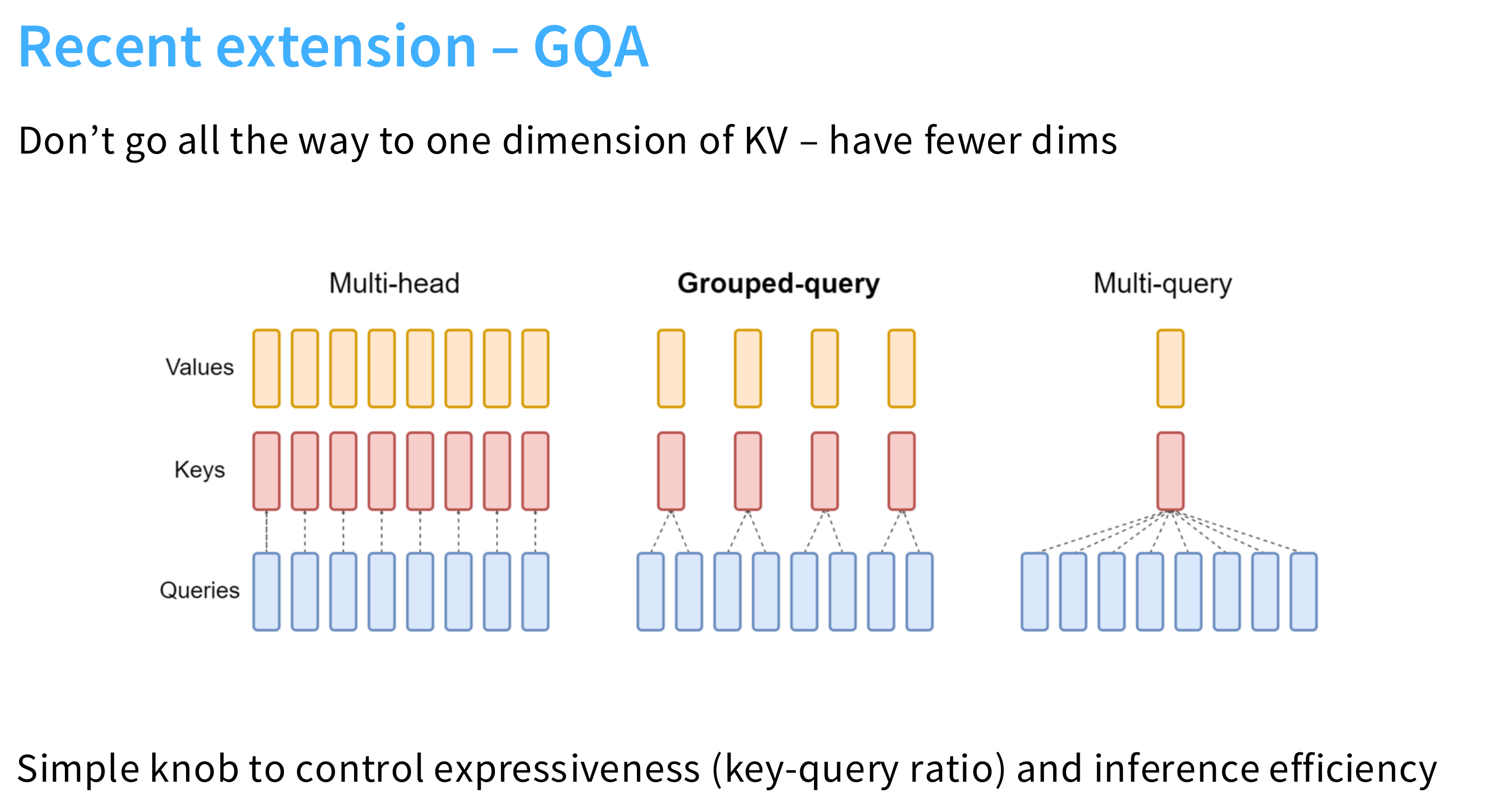
GQA（Grouped-Query Attention）

核心思想：

  • 折中方案：介于 MHA 和 MQA 之间。
  • 将多个头 分组，每组共享一组 K 和 V。
  • 例如：如果有 32 个头，分成 4 组，每组 8 个头，那么就有 4 个不同的 K 和 V。

image-20250729144756812

对比总结

方法 Query Key Value KV Cache 大小 表达能力 推理效率
MHA（标准） 每头独立 每头独立 每头独立 高（H 倍） 最强 最低
GQA 每头独立 每组共享 每组共享 中等（G 倍） 较强 高
MQA 每头独立 全局共享 全局共享 最低（1 倍） 较弱 最高

H：总头数，G：组数（1 ≤ G ≤ H）

Sparse / sliding window attention

稀疏注意力（Sparse Attention）

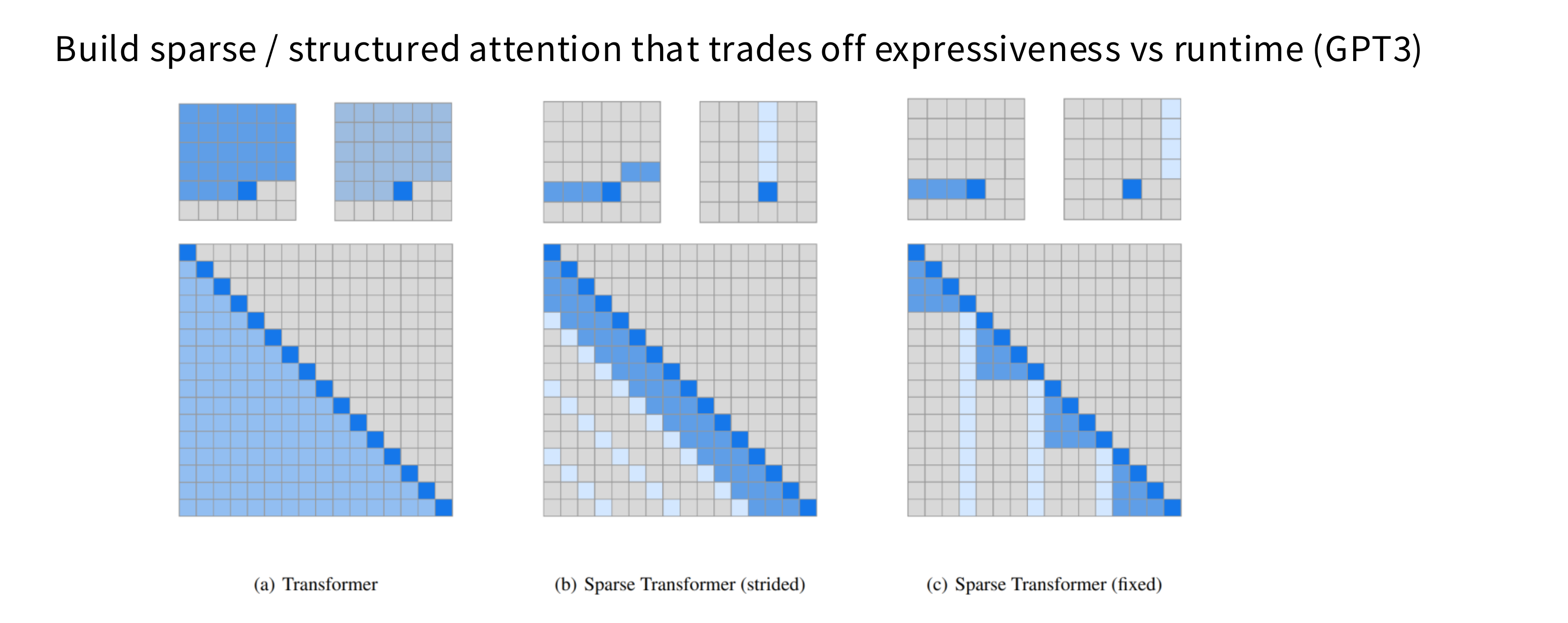
image-20250729145142611

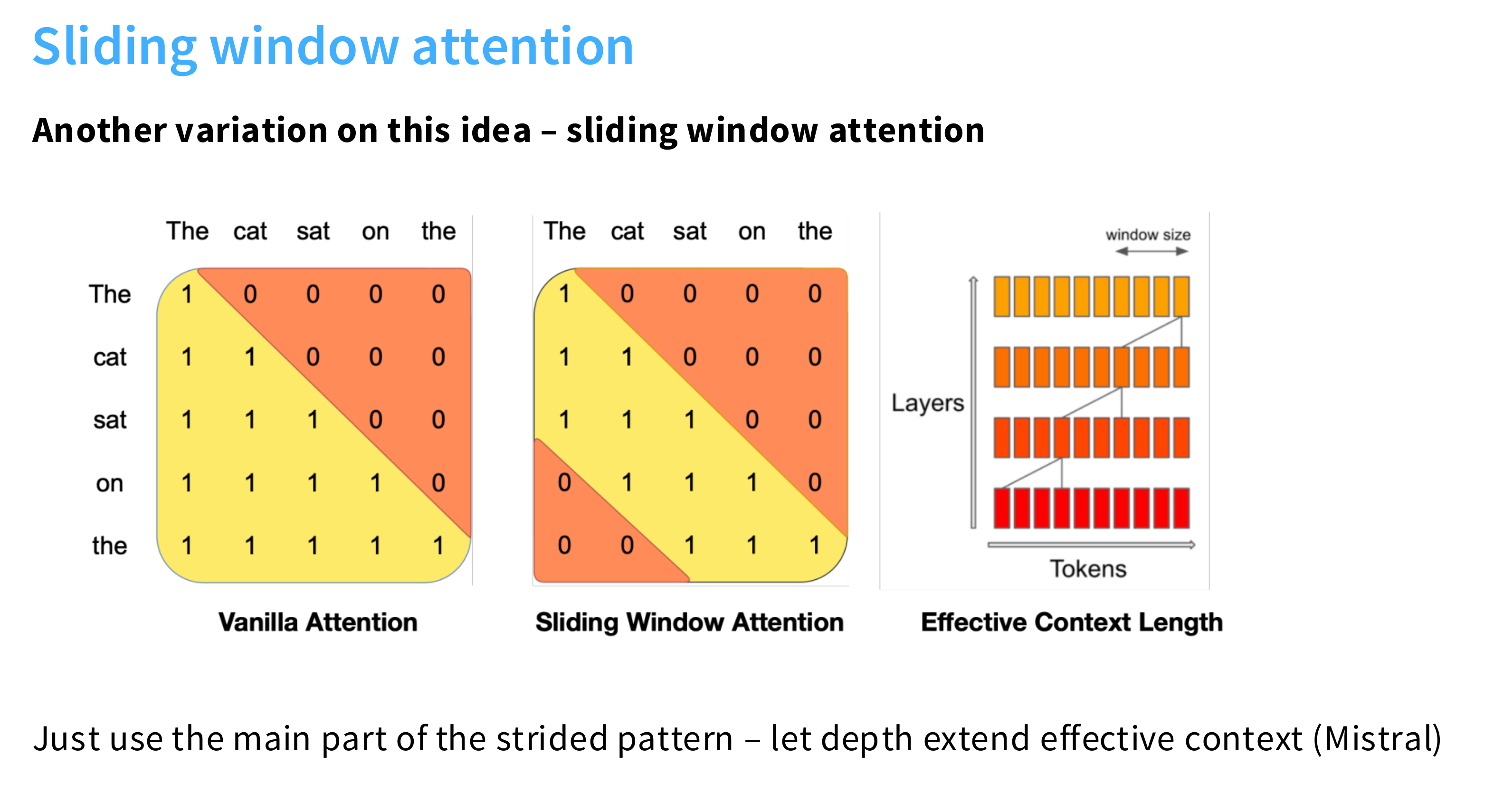
SWA滑动窗口注意力（Sliding Window Attention）

具体来说：

  • 对于位置 i 的 token，它只与前后 w 个 token 计算注意力（即一个大小为 2w+1 的“滑动窗口”）。
  • 窗口随位置移动，像卷积一样滑过序列。

示例：

  • 如果窗口大小是 512，则每个 token 最多与前后 256 个 token 注意。
  • 复杂度从 O(n2) 降到 O(n×w) ，当 w≪n 时大幅降低。

特点：

  • 局部建模能力强（适合局部依赖，如语法、局部上下文）。
  • 无法建模远距离依赖（比如首尾 token 无法直接交互）。
  • 实现简单，常用于长文本模型的局部注意力部分。

image-20250729145203562

interleave ‘full’ and ‘LR’ attention

  • ‘Full’ attention：全注意力（即每个 token 可以看到整个上下文）
  • ‘LR’ attention：这里 LR 指 Long-Range，但实际指的是 受限注意力，比如 Sliding Window Attention (SWA)，用于局部上下文建模。

交替使用全注意力（Full Attention）和局部/受限注意力（如滑动窗口注意力 SWA）”，以在效率和长距离依赖建模能力之间取得平衡。

From Cohere Command A – Every 4th layer is a full attention

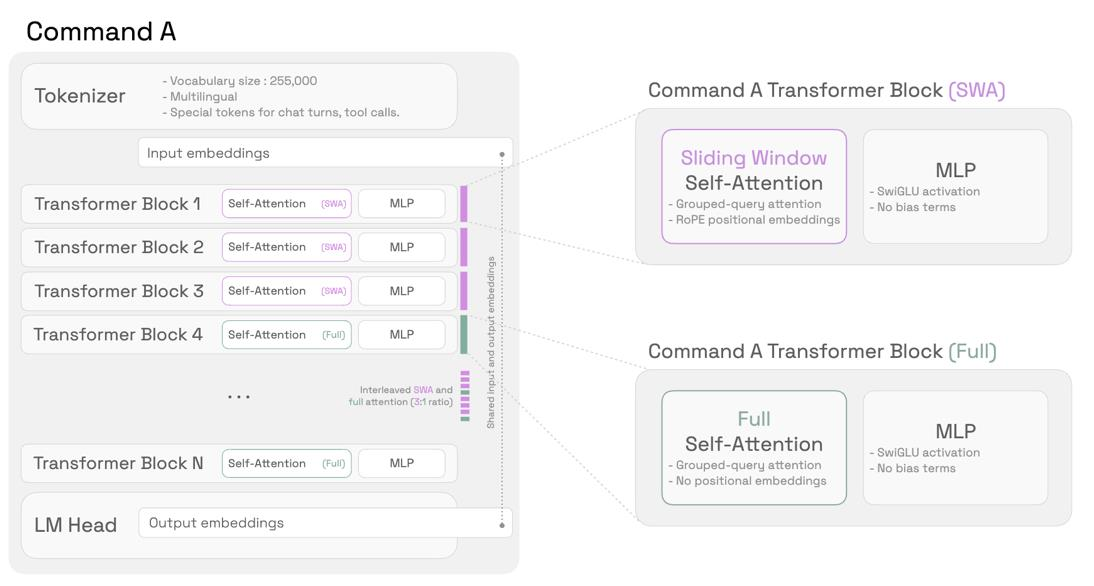
image-20250729145455753

Long-range info via NoPE, short-range info via RoPE + SWA